Resistors connected in series

Combining resistors in series has the basic property of adding up their resistances. Series components also split up voltage. The series resistors will have a percentage of the total voltage across them that is based on their percentage of the total resistance, which is calculated after having removed the voltage from the semiconductor drops.

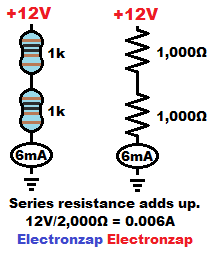
Series resistance basic circuit schematic diagram example image
Series resistance basic circuit schematic diagram example image

Become a Patron!

12 volts across 2,000 ohms of resistance will pass 12V/2,000Ω = 0.006A of current. Which is usually converted to 6mA.

If you measure current through two 1,000 ohm resistors that are connected end to end, usually referred to as being in series, while powering them with 12V, then you will measure about 6mA of current flowing through the circuit. Their resistances add up for a total of 2000Ω as far as the rest of the circuit is concerned.

You can also measure the voltage across each resist0r. Finding that there is about 6 volts across two equal value resistors in series, even though the whole circuit is powered with 12v. The series resistors divide up the total voltage based on each resistor’s percentage of the total resistance.

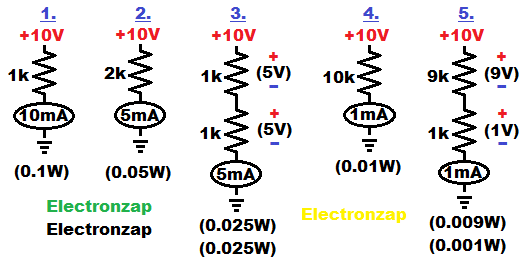
single versus series resistors schematic diagram example circuits by electronzap
single versus series resistors schematic diagram example circuits by electronzap

I added some more example circuits above, which includes wattage calculations. Every series component that helps reduces the current of the circuit by absorbing some of the voltage, will share the burden of heat dissipation. The series component with the most voltage across it, will generate the most heat, since all series components are passing the same amount of current.

  • 10V/1,000Ω = 0.01A (10mA). 0.01A x 10V = 0.1 watt of power (waste heat) that a single resistor has to dissipate.
  • 10V/2,000Ω = 0.005A (5mA). 0.005A x 10V = 0.05W of power that needs to be dissipated.
  • 10V across 10k (10,000 ohms) of resistance will pass 0.001A 0r 1mA of current. If a 9k resistor is used as part of that 10k total resistance, then it will have 90% of the total voltage across it. Therefore, it will get 9 times hotter than a 1k resistor in series with it.

Good pages to check out next:

 To support this site, check out the following links:

Home page

  • Information on this site is not guaranteed to be accurate. Always consult the manufacturer info/datasheet of parts you use. Research the proper safety precautions for everything you do.
  • Electronzap is a participant in the Amazon Services LLC Associates Program, an affiliate advertising program designed to provide a means for sites to earn advertising fees by advertising and linking to amazon.com.